Newton’s Method - SOLUTIONS#

Another root-finding algorithm that is often used is called Newton’s method or the Newton-Raphson method.

It is a simple iterative algorithm, based on the idea that we draw a tangent line to $f(x)$ (by computing the derivative of $f(x)$) sufficiently near to a root of $f(x)=0$, then the tangent will cut the axis nearer to the root than the original point.

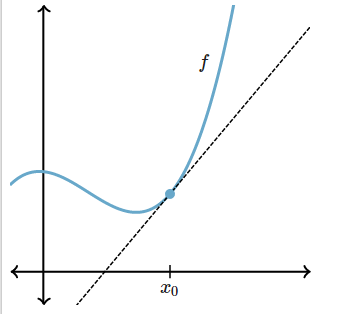Newtons's method graphical illustration The equation of a tangent line to a curve $f$ at point $x_0$ is given by

\[ y = f^{\prime}(x_0)(x - x_0) + f(x_0)\]

The following code (needs to be run in Colab) gives an interative illustration of generating this tangent line.

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, interactive, fixed

def f(x): # the curve f
  return (x - 3)**2 - 4

def df(x): # derivative of f
  return 2*(x - 3)


def tangent(x0): # plotting the curve f and the tangent line to f at point x0
    x = np.linspace(0, 6, num = 1000)
    plt.plot(x, f(x))
    plt.plot(x, df(x0)*(x - x0) + f(x0))
    plt.ylim(-5, 5) # limits of y axis
    plt.show()

x0_inc = 0.01 #this is the increment in x0
interactive_plot = interactive(tangent, x0 = (0, 5.0, x0_inc))
interactive_plot

You can also see https://www.geogebra.org/m/n6KXp4hE for another interactive demonstration of this.

Some formal theory#

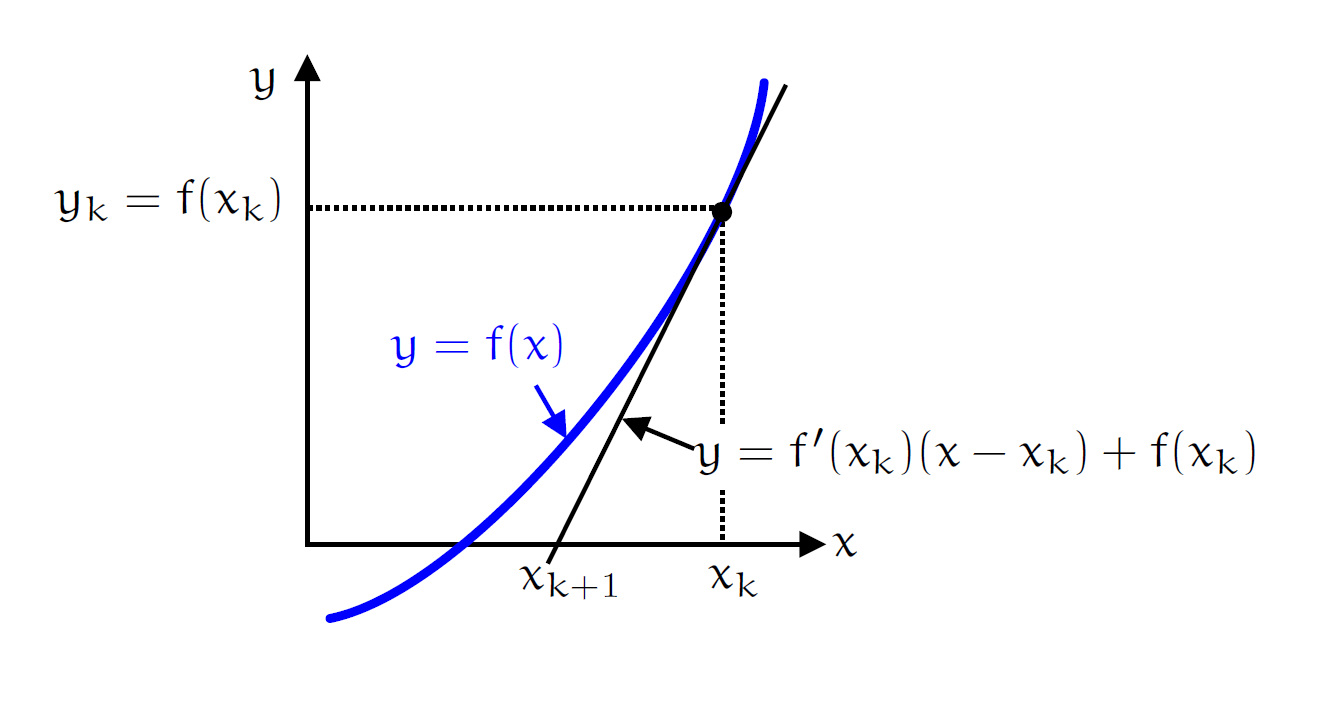
Newton's theory illustration of tangent lines

When the tangent crosses the $x$-axis $y=0$. Hence, at this point we have the equation

\[ 0 = f^{\prime}(x_0)(x - x_0) + f(x_0)\]

Replacing $x_0$ with the current $x_k$ point in the $k$-th iteration, and $x$ with $x_{k+1}$ we obtain

\[0 = f^{\prime}(x_k)(x_{k+1} - x_k) + f(x_k)\]

\[f(x_k) = f^{\prime}(x_k)(x_k - x_{k+1})\]

Denote the current approximate solution as $x_k$ and the new point as $x_{k+1}$ the above figure shows that the gradient of the tangent is $$ f^{\prime}(x_k) = \frac{f(x_k)}{x_k-x_{k+1}}$$

We can rearrange $$ f^{\prime}(x_k) = \frac{f(x_k)}{x_k-x_{k+1}}$$ into $$ x_{k+1} = x_{k} - \frac{f(x_k)}{f^{\prime}(x_k)}.$$

Main, important formula for coding this!#

The main formula in Newton’s method is $$ x_{k+1} = x_{k} - \frac{f(x_k)}{f^{\prime}(x_k)}.$$

Step 1#

Now let’s start implementing this. First, write a function that makes one iteration of Newton’s method. That is, the function should take a value of $x$ ($x_k$), the function object $f$ and it’s derivative $f'$ and return the next value of $x$ ($x_{k+1}$)

def newton_step(xk, f, df):
    return xk - f(xk)/df(xk)

Testing this code#

Now test this out with a specific function. Find the root of:

\[x - e^{-2x} = 0\]

Now use netwon_step with $x_0 = 0.5$ to obtain the above $x_1$, $x_2$ and $x_3$ also print $f_1$, $f_2$, $f_3$ and $f_1^{\prime}$, $f_2^{\prime}$

import math

def f(x):
    # Define the function here
    return x - math.exp(-2*x)

def df(x):
    # Define the derivative of the function here.
    return 1 + 2*math.exp(-2*x)

    
x0 = 0.5
x1 = newton_step(x0, f, df)
x2 = newton_step(x1, f, df)
x3 = newton_step(x2, f, df)


print("x1 is {0}, it should be 0.423883".format(np.round(x1, 6)))
print("x2 is {0}, it should be 0.4263".format(np.round(x2, 6)))
print("x3 is {0}, it should be 0.426303".format(np.round(x3, 6)))

print(f"f(x1) is {f(x1)}")
print(f"f(x2) is {f(x2)}")
print(f"f(x3) is {f(x3)}")

print(f"df(x1) is {df(x1)}")
print(f"df(x2) is {df(x2)}")

x1 is 0.423883, it should be 0.423883
x2 is 0.4263, it should be 0.4263
x3 is 0.426303, it should be 0.426303
f(x1) is -0.004487630303117329
f(x2) is -4.996680327662428e-06
f(x3) is -6.2021499047659745e-12
df(x1) is 1.8567414910745765
df(x2) is 1.852610101161614

It definitely feels like a for loop, or a while loop would be nicer if needing to iterate this a lot of times!

Step 2#

Complete a function, newton, with inputs

a float $\verb|x0|$ (initial approximation),
a function $\verb|f|$,
its derivative $\verb|df|$,
and $n$.

Your function should perform $n$ interations of the newton_step function before calculating the final approximation to the root of $f$. An outline of the function is given below:

def newton(x0, f, df, n):
    #Please write your code here
    x = x0
    for _ in range(n):
        x = newton_step(x, f, df)
    return x

Testing your answers#

Run the cell below to test if this is correct

x0 = 10.0
n = 1000

def test_f1(x):
    return np.sin(x)-np.exp(x)

def dtest_f1(x):
    return np.cos(x)-np.exp(x)
    
def test_f2(x):
    return x-50

def dtest_f2(x):
    return 1

def test_f3(x):
    return np.sinh(x) - np.sin(x)

def dtest_f3(x):
    return np.cosh(x) - np.cos(x)

assert np.isclose(newton(x0, test_f1, dtest_f1, n), -9.424858653775413)
assert np.isclose(newton(x0, test_f3, dtest_f3, n), 0, atol=1E-6)

Step 3: Using a while loop#

Complete a function, newton2, with inputs

a float $\verb|x0|$ (initial approximation),
a function $\verb|f|$,
its derivative $\verb|df|$,
a float $\verb|eps|$ (approximation error)

Iterate the newton_step function until the difference between $x_k$ and $x_{k+1}$ lies in the interval $(-\verb|eps|, \verb|eps|)$.

Your function should return

the root,
and the step $k$, when the loop was broken.

def newton2(x0, f, df, eps):
    #Please write your code here
    x = x0
    count = 0
    while 1:
        xn = newton_step(x, f, df)
        count += 1
        if abs(xn - x) < eps:
            return xn, count
        x = xn

Testing your answers#

As before, please run the cell below to test if your function is correct!

eps = 0.01
x0 = 10.0

print(newton2(x0, test_f3, dtest_f3, eps) )

ans1, count1 = newton2(x0, test_f1, dtest_f1, eps)
assert count1 == 16
assert np.isclose(ans1, (-9.424858653775413))
ans2, count2 = newton2(x0, test_f3, dtest_f3, eps)
assert count2 == 20
assert np.isclose(ans2, 0.0163818089496369)

(0.016381808949641218, 20)

Exercise 1#

Consider the equation \begin{equation} \tan^{-1}x=0.5x. \end{equation}

Re-arrange the equation into the form $f_1(x)=0$ and hence write a Python function $\verb|f1|$ for $f_1$.
Differentiate $f_1(x)$ with respect to $x$ and hence write a Python function, $\verb|df1|$ for the derivative $f_1'(x)$.
Using a starting point of $3$, apply your newton2 function in order to find a root of the equation to $9$ decimal places.

How many steps were needed?

The function $\tan^{-1}$ is implemented in the numpy library, under the name np.arctan.

def f1(x):
    #Please write your code here
    return math.atan(x) - 0.5*x

def df1(x):
    #Please write your code here
    return 1/(x**2 + 1) - 0.5

x0 = 3 #Please write your code here
eps = 1E-9 #Please write your code here

x, k = newton2(x0, f1, df1, eps)
print(x, k)

2.3311223704144224 5

Testing your code#

Run the cell below!

assert abs(f1(x0)) == 0.25095422760174557
assert abs(df1(x0)) == 0.4
assert x0 == 3
assert eps == 10**(-9)
assert np.isclose(x, 2.331122370414423)
assert k == 5

Exercise 2#

Use your Newton method to find the root of the following equation as accurately as you can.

\begin{equation} x^5+3=8x \quad{}\mbox{near}\quad{} x=0.5, \end{equation}

Re-arrange the equation into the form $f_2(x)=0$ and hence write a Python function $\verb|f2|$ for $f_2$.
Differentiate $f_2(x)$ with respect to $x$ and hence write a Python function, $\verb|df2|$ for the derivative $f_2'(x)$.
Using a starting point of $0.5$, apply your newton2 function in order to find a root of the equation to $9$ decimal places.

How many steps were needed?

def f2(x):
    #Please write your code here
    return x**5 + 3 - 8*x

def df2(x):
    #Please write your code here
    return 5*x**4 - 8

x0 = 0.5 #Please write your code here
eps = 1E-9 #Please write your code here

x, k = newton2(x0, f2, df2, eps)
print(x, k)

0.37593863077555095 4

Testing your code#

Run the cell!

assert abs(f2(x0)) == 0.96875
assert abs(df2(x0)) == 7.6875
assert x0 ==0.5
assert eps == 10**(-9)
assert np.isclose(x, 0.37593863077555095)
assert k == 4

M24568 and M20741 Intro to CompSMAP

Newton’s Method - SOLUTIONS

Contents

Newton’s Method - SOLUTIONS#

Some formal theory#

Main, important formula for coding this!#

Step 1#

Testing this code#

Step 2#

Testing your answers#

Step 3: Using a while loop#

Testing your answers#

Exercise 1#

Testing your code#

Exercise 2#

Testing your code#