Bolzano’s Theorem - SOLUTIONS

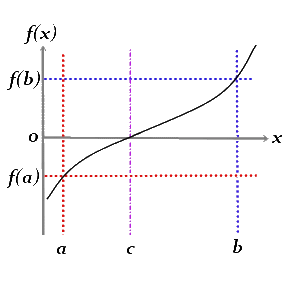
Bolzano’s theorem states: For a continuous function \(f\), given \(a\), \(b \in \mathbb{R}\) such that \(a<b\), if \(f(a)\) and \(f(b)\) have opposite signs, that is, \(f(a)f(b)<0\), then the equation $\( f(x) = 0\)\( has a solution (a root) between \)a\( and \)b$.

… This may be hard to parse, but is really quite intuitive. If the function has a value less than 0 at position \(x_1\) and a value greater than 0 at position \(x_2\), and the function is continuous, at some point between \(x_1\) and \(x_2\) the function must have a value of 0.

Exercise 2.1

Can you see why this theorem does not work if the function is discontinuous? Think about it and try to type your explanation below.

A discontinuous function does not have to go through 0. For e.g. \(1/x\) is positive above \(x=0\) and negative below \(x=0\) but does not cross 0 to swap from positive to negative, it has a discontinuity at \(x=0\).

Exercise 2.2

In the cell below define a function $\( f(x) = x^5+6x^3+x-17.\)\( Then use Bolzano's theorem to show that \)f\( has a root in the interval \)\left[1, \frac{3}{2}\right]$.

You may want to evaluate \(f\) at both ends of the interval, if the value of \(f\) changes sign then it proves that \(f\) has a root in this interval.

def f(x):
    return x**5 + 6*x**3 + x - 17

print(f(1), f(1.5))

print("As one of these is negative, and one is positive, there must be a root in this interval")

-9 12.34375
As one of these is negative, and one is positive, there must be a root in this interval