Writing a root finding algorithm using the bisection method - SOLUTIONS#

Theory and problem statement#

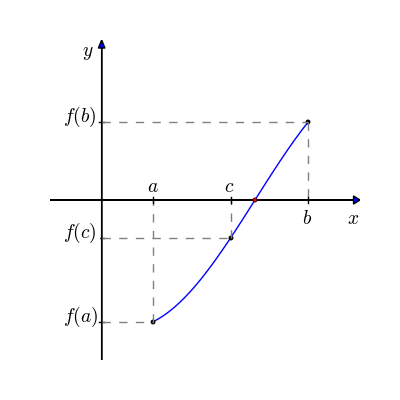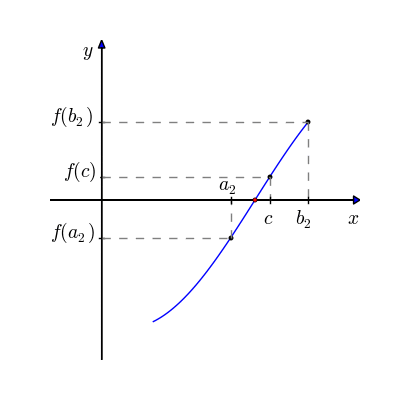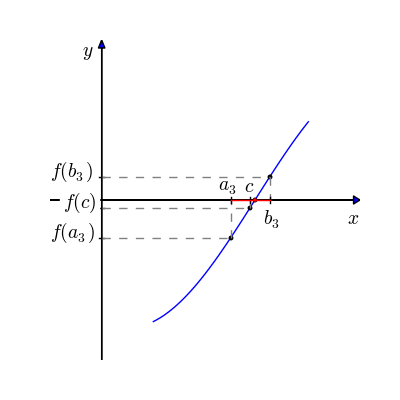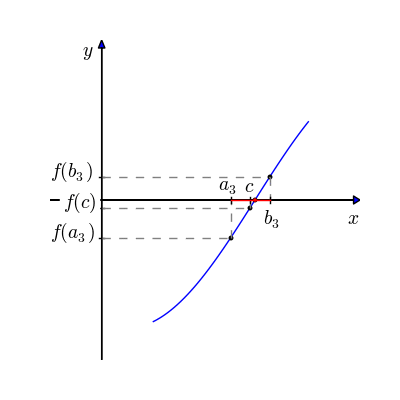
Bolzano’s theorem offers a way of writing a numerical root finding algorithm. If we have identified a point where the function is above 0 ($x_1$), and a point where the function is below 0 ($x_2$), we can just try points in the middle to find where it crosses over. A simple way to do this is to test the value of the function halfway between $x_1$ and $x_2$ at the point $x_m$. If that value is also above 0, then we know the root is beween $x_m$ and $x_2$, is it is below 0 then the root is between $x_1$ and $x_m$. We can repeat that process until we’ve found a point where the function is “close enough” to 0.

An illustration of this process is shown here

Animated GIF of Bisection method

or see the interactive example here:

https://www.geogebra.org/m/XndvAujc

Let’s state the problem again more formally:

PROBLEM: Given a continuous function $f$ defined on the interval $[a, b]$ for $-\infty<a<b<\infty$ we wish to find a $x \in [a, b]$ such that $$f(x) = 0.$$ Let us assume that $f(a)f(b)<0$ and so by Bolzano's Theorem we know that such a value of $x$ exists!

Approximation We provide a method to approximate $x$, so we need to specify the error $\varepsilon$ in approximation, e.g. if $$ f(x) \in (-\varepsilon, \varepsilon) \ \mbox{ or equivalently } \ |f(x)| < \varepsilon$$ then we wish to accept $x$ as the solution.

Let’s now implement this in code. We’ll do this step by step, and ask you to write the blocks needed as we go.

IMPLEMENTATION STEP 1#

Define $c= \frac{a+b}{2}$, the midpoint of the interval $[a,b]$.

Complete a function, midpoint, with two inputs, $a$ and $b$, which returns the mid-point, $c$, of the interval $[a, b]$. Hint: the midpoint is the average value.

def midpoint(a, b):
    return (a+b)/2

Testing your answers#

If the below test cases do not return AssertionError then your solution to Exercise 3.1 is correct. So shift+enter through all the cell below.

import numpy as np
a1, b1 = 0, 2
a2, b2 = -3, 3
a3, b3 = np.sqrt(2), 2

assert midpoint(a1, b1) == 1.0
assert midpoint(a2, b2) == 0.0
assert midpoint(a3, b3) == np.sqrt(2)/2+1

Step 2#

Check if $f(c) \neq 0$, if $|f(c)|$ is sufficiently small then return $c$ as your answer

In the cell below complete the function if_root so that it has three inputs:

$c$, a float,
$f$, a function of one numerical variable that has numerical output,
$eps$, a float, that represents the error in approxiation.

If should return True if $|f(c)| < \varepsilon$, else it should return False. For absolute value please use $\verb|abs|$.

def is_root(c, f, eps):
    # Please add function content
    if abs(f(c)) < eps:
        return True
    return False

Testing your answers#

Again run the cell below. An AssertionError means that your function is not working!

import numpy as np
c1 = 0
c2 = np.pi/2.
f1 = np.cos
f2 = np.sin
eps = 1E-5

assert is_root(c1, f1, eps) == False
assert is_root(c1, f2, eps) == True
assert is_root(c2, f1, eps) == True
assert is_root(c2, f2, eps) == False

Step 3#

Check if $f(a)f(c)<0$ if so then replace $b$ with $c$ otherwise replace $a$ with $c$.

In the cell below complete the function new_interval so that it has four inputs,

$a$ a float, beginning of interval,
$b$ a float, end of interval,
$c$ a float, a point inside $[a, b]$,
$f$ a function of one numerical variable that has numerical output.

It should return a tuple (a pair) of numbers which represents the new interval according to Step 3.

def new_interval(a, b, c, f):
    # Complete code here
    if f(a) * f(c) < 0:
        return (a,c)
    else:
        return (c,b)

import numpy as np
eps = 1E-5

assert new_interval(-1, 1, 0.5, np.sin) == (-1,0.5)
assert new_interval(-1, 1, -0.5, np.sin) == (-0.5, 1)
assert new_interval(1, 2, 1.5, np.cos) == (1.5,2)
assert new_interval(1, 3, 2, np.cos) == (1, 2)

Step 4#

These previous 3 steps represent a single iteration of the bisection method. Let’s now string these together to carry out one iteration.

Complete a function, bisection_step, with inputs $f$ (supposed to be a function), $a$, $b$, and $eps$ that performs a single step of the bisection method, returning the endpoints of the new interval. An outline of the function is given below:

def bisection_step(f, a, b, eps):
    # Call the function midpoint to get a value for c
    c = midpoint(a,b)
    
    # Check if f(c) is small enough to be a root (using the is_root function). If it is, return (c,c)
    if is_root(c, f, eps):
        return (c,c)
    
    # Otherwise call new_interval to find the new interval, and return that.
    return new_interval(a, b, c, f)

Testing your answers#

If the below test cases do not return AssertionError then your code is correct so far. So shift+enter the cell below.

def f1(x):
    return x

def f2(x):
    return np.cos(x)

def f3(x):
    return x-np.sqrt(2)

a1, b1 = -1.0, 2.0
a2, b2 = 0.2, 3.0
a3, b3 = 0.0, 2.0
a4, b4 = -1, 1
eps = 1E-5

assert bisection_step(f1, a1, b1, eps) == (-1.0, 0.5)
assert bisection_step(f2, a2, b2, eps) == (0.2, 1.6)
assert bisection_step(f3, a3, b3, eps) == (1.0, 2.0)
assert bisection_step(f1, a4, b4, eps) == (0., 0.)

Step 5#

Now we want to be able to run this function multiple steps. First we try running it a fixed number of iterations, using a for loop

Complete a function, bisection, with inputs $f$ (supposed to be a function), $a$, $b$, $eps$ and $n$ that performs the bisection step $n$ times. The final approximation to the root is then taken as the midpoint of the interval obtained after $n$ iterations.

Hints: you will need a for loop. Your single-step bisection code then needs to be inside the loop, i.e., it needs to be indented in the loop. Take care that the calculation for the final approximation to the root is done after the loop. You can update the values of $a$ and $b$ in the loop by using a, b = bisectionStep(f, a, b).

An outline of the function is given below:

def bisection(f, a, b, eps, n):
    # perform bisection_step n times here
    # updating the values a, b each time...
    for k in range(n):
        a,b = bisection_step(f, a, b, eps)
    # calculate and return the final approximation to the root.
    c = midpoint(a,b)
    return c

Testing your answers#

If the below test cases do not return AssertionError then your solution is correct. So shift+enter the cell below.

n1 = 5
n2 = 10
n3 = 15
eps = 1E-5

assert bisection(f1, a1, b1, eps, n1) == -0.015625
assert bisection(f2, a2, b2, eps, n2) == 1.5712890625
assert bisection(f3, a3, b3, eps, n3) == 1.414215087890625

Step 6#

Now let’s improve our algorithm. In general we don’t know how many steps are required to reach a root that is accurate to within the accuracy ($eps$) specified. We want to take exactly the number of steps that are needed to obtain the answer to within the specified accuracy (not too many, not too few).

This is a perfect use case for a while loop. We can just iterate our algorithm until the is_root function returns True, this will then mean that our boundary lower and upper values are the same, and we can stop at this point.

So let’s write a function bisection2 with inputs $f$ (supposed to be a function), $a$, $b$ and $eps$ that performs the bisection step the required number of times to obtain a root within $eps$ of the true value and returns that root.

def bisection2(f, a, b, eps):
    # perform bisection_step n times here
    # updating the values a, b each time...
    while a != b:
        a,b = bisection_step(f, a, b, eps)
    return a

Testing your answers#

If the below test cases do not return AssertionError then your solution is correct. So shift+enter the cell below.

def f1(x):
    return x-np.sin(x)

def f2(x):
    return np.tan(x/4) -1

a1, b1, eps1 = 20, 40, 0.001
a2, b2, eps2 = 3.1, 3.3, 0.0001

print(bisection2(f1, a1, b1, eps1), bisection2(f2, a2, b2, eps2))

assert np.round(bisection2(f1, a1, b1, eps1),3) == 40.000
assert np.round(bisection2(f2, a2, b2, eps2),4) == 3.1414

40.0 3.14140625

Example#

Now we use the bisection methods that we programmed to find the root of $$r(x) = x^{11}-4x^7+3x^5+11x^3+12x^2+x-170$$ in the interval $[-20, 20]$.

def r(x):
    return x**11 - 4 * x**7 + 3 * x**5 + 11 * x**3 + 12 * x**2 + x - 170

a = -20
b = 20
eps = 0.000001
print(r(a), r(b))

-204794889683390 204794889692650

root = bisection2(r, a, b, eps)
print(root)

1.5921310149133205

print(r(root))

-8.724785516278644e-08

Exercise#

Use Python to show that the equation $$\cos x-\ln x+0.8=0,$$ has a root in the interval $[1,2]$.

Write the above equation as $f(x) = 0$, and define f in Python.
Use your function bisection with large $n$ or bisection2 to calculate the root.

# HINT: The root is 1.790216, make sure you get that number back!
import math

def f(x):
    return math.cos(x) - math.log(x) + 0.8

print(bisection2(f, 1, 2, 0.000000000001))

1.7902163063372427

M24568 and M20741 Intro to CompSMAP

Writing a root finding algorithm using the bisection method - SOLUTIONS

Contents

Writing a root finding algorithm using the bisection method - SOLUTIONS#

Theory and problem statement#

IMPLEMENTATION STEP 1#

Testing your answers#

Step 2#

Testing your answers#

Step 3#

Step 4#

Testing your answers#

Step 5#

Testing your answers#

Step 6#

Testing your answers#

Example#

Exercise#