Continuous functions - SOLUTIONS

A continuous function is one whose range of values can be drawn without lifting the pencil from the paper.

A continuous function does not have jumps, or discontinuities, its graph is a single unbroken curve.

Examples of continuous functions

• Polynomials. A polynomial is a function that is defined/built from constants and symbols/variables by means of addition, multiplication and exponentiation to a non-negative integer power. General form of a polynomial: \(p(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1 x + a_0\), where \(n \in \{1, 2, \ldots\}\) and \(a_n\) are real numbers, are continuous functions,

• trygonometric functions such as \(\sin(x)\), \(\cos(x)\) are continuous functions,

• exponential functions, e.,g., \(2^x, 3^x\) or \(e^x\) are continuous functions.

Linear combinations (these includes sums and differences) of continuous functions are continuous functions.

Polynomials - can you identify them?

Which of the below functions are polynomials?

• \(f(x) = 2x^3+2x+\frac{1}{x^2}\),

• \(g(x) = x^2+7x\),

• \(h(x) = x^5\),

• \(k(x) = \frac{2x^2+5x}{1+2x}\).

\(g(x)\) and \(h(x)\) are polynomials. The other two are not.

Examples of discontinuous functions

In discontinuous functions we can see gaps in the curve. For example $\(f(x) = \frac{1}{x-1}\)$

is not continous at \(x=1\).

The function \(f(x) = x^{-1}\) is not continuous at \(x=0\); negative powers bring discontinuities.

If a function is not defined at some points, e.g., like \(x^{-1}\) is not defined at zero, in Python if you call such function at this point it will raise ZeroDivisionError.

def f(x):
    return x**(-1)

print(f(0))

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
Input In [1], in <module>
      1 def f(x):
      2     return x**(-1)
----> 4 print(f(0))

Input In [1], in f(x)
      1 def f(x):
----> 2     return x**(-1)

ZeroDivisionError: 0.0 cannot be raised to a negative power

However, discontinuous functions don’t always raise errors at the discontinuity.

def f(x):
    if x >0:
        return x**2
    else:
        return x+5

import numpy as np
import matplotlib.pyplot as plt

arguments = np.linspace(-5, 5, num=1000) # an array of arguments [x1, x2,..., xn]
vals = []
for value in arguments:
    vals.append(f(value))
plt.plot(arguments, vals)
plt.show()

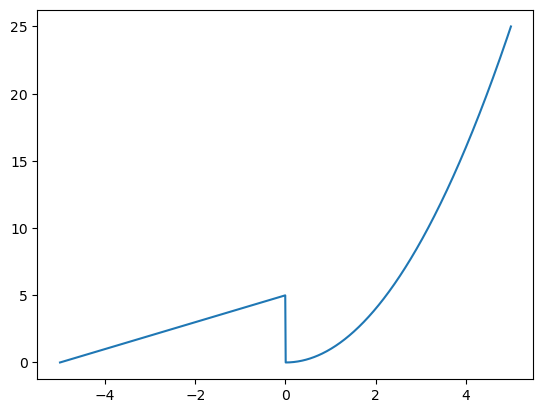
There is a jump at \(0\). The function has an instantaneous jump from 5 to 0. This function is discontinuous.

Exercise 1.1

Give an example of a function that is not continuous and plot its graphs from which we can clearly see the discontinuity.

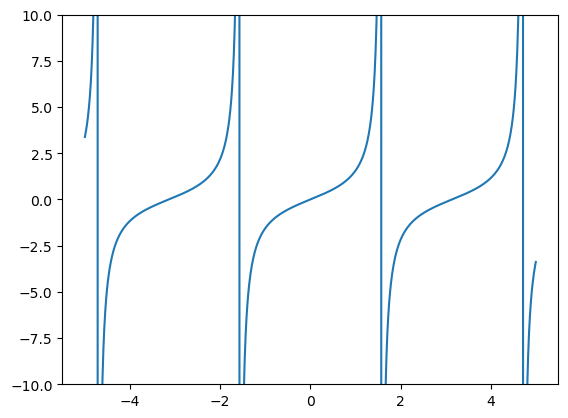
# tan(x) is a discontinuous function, with a discontinuities at (pi/2 + n*pi), where n is any integer.

import numpy as np
import matplotlib.pyplot as plt

arguments = np.linspace(-5, 5, num=1000) # an array of arguments [x1, x2,..., xn]
vals = np.tan(arguments)
plt.plot(arguments, vals)
plt.ylim([-10,10])
plt.show()