Adding Interactive Elements: Sliders

In order to obtain some interactive features we have to import the following library:

from ipywidgets import interact, interactive, fixed

import matplotlib.pyplot as plt
import numpy as np

Let’s define some function of two variables, and a value c that is fixed.

def g(x, y, c):
    return x**2+y**2 + c

g(4,5,6)

47

To interact with our values of x and y to change the output of \(g(x,y)\), we can make use of sliders:

interact(g, x=(0,10), y=(-10, 0), c=fixed(5))

<function __main__.g(x, y, c)>

Now you can use the sliders above to check different values of \(g\) for different inputs \(x\) and \(y\).

You could also have input an array of values for \(c\) as follows:

import numpy as np
cvals = np.linspace(1,5,5)
interact(g, x=(0,10), y=(-10, 0), c=fixed(cvals))

<function __main__.g(x, y, c)>

Suppose we want non-integer changes for our slider-generated values of \(x\) and \(y\). This can be dones as follows:

x = np.linspace(1,5,5)
interact(g, x=(0,10,0.5), y=(-10, 0, 0.5), c=fixed(x))

<function __main__.g(x, y, c)>

Exercise 4.1

Let’s make a plot of the function \( x(t) = \sin{(\omega t - \phi)} \), using sliders to control the values of \(\omega\) and \(\phi\):

1. Create an array of \(t\) values between 0 and \(5\pi\).

2. Add sliders called omega and phi to control the values of \(\omega\) and \(\phi\).

3. Complete the function func_t to calculate \(x(t)\), using \(t\), \(\omega\) and \(\phi\) as inputs.

4. Modify the command for the plot of \(x(t)\) versus \(t\) to add appropriate labels to your plot.

Adding error bars

When performing an experiment, any measurements will have a degree of uncertainty. We represent this uncertainty on plots using error bars.

In this example we will go over plotting uncertainties in various ways:

• y errorbars

• x errorbars

• x and y errorbars

We can plot errorbars on our data as follows:

ax.errorbar(x,y,xerr=A,yerr=B)

An excellent demo of errorbar plotting can be found in the matplotlib gallery: https://matplotlib.org/examples/statistics/errorbar_demo_features.html

If your data has asymmetric errorbars, documentation on this can be found at: https://matplotlib.org/examples/statistics/errorbar_demo_features.html

For example, for fixed size errorbars (each data point has the same error)

#generate some data to plot.
x = np.linspace(0.,20.,20)
y = (3*x**2) - (0.25*x**3) - 5.

fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111)
#ax.scatter(x,y)

#Add error bars
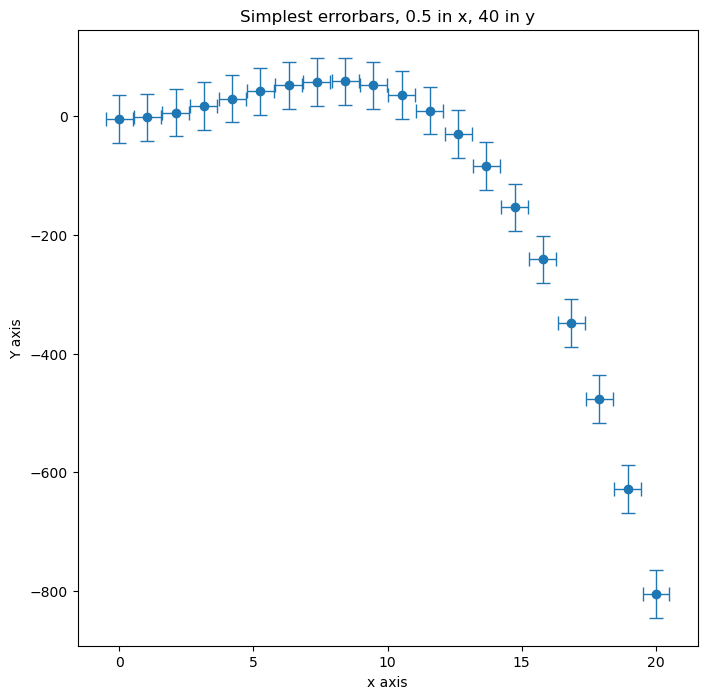
ax.errorbar(x, y, xerr=0.5, yerr=40, fmt='o', capsize=5, elinewidth=1)

ax.set_title("Simplest errorbars, 0.5 in x, 40 in y");
ax.set_xlabel("x axis")
ax.set_ylabel("Y axis")
plt.show()