Bolzano’s Theorem

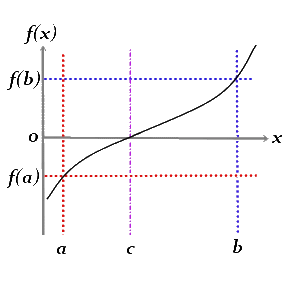
Bolzano’s theorem states: For a continuous function \(f\), given \(a\), \(b \in \mathbb{R}\) such that \(a<b\), if \(f(a)\) and \(f(b)\) have opposite signs, that is, \(f(a)f(b)<0\), then the equation $\( f(x) = 0\)\( has a solution (a root) between \)a\( and \)b$.

… This may be hard to parse, but is really quite intuitive. If the function has a value less than 0 at position \(x_1\) and a value greater than 0 at position \(x_2\), and the function is continuous, at some point between \(x_1\) and \(x_2\) the function must have a value of 0.

Exercise 2.1

Can you see why this theorem does not work if the function is discontinuous? Think about it and try to type your explanation below.

Write your answer here (Double click on this field)

Exercise 2.2

In the cell below define a function $\( f(x) = x^5+6x^3+x-17.\)\( Then use Bolzano's theorem to show that \)f\( has a root in the interval \)\left[1, \frac{3}{2}\right]$.

You may want to evaluate \(f\) at both ends of the interval, if the value of \(f\) changes sign then it proves that \(f\) has a root in this interval.